深谷技术 | 基于拉格朗日公式法的SCARA机器人动力学建模

       SCARA机器人（Selective Compliance Assembly Robot Arm，选择性柔顺装配机械臂）是一种水平多关节工业机器人，其核心结构由基座、水平旋转关节、垂直移动轴及末端执行器构成，凭借水平方向的柔顺性适应微小位置偏差，同时垂直方向保持高刚性，实现了±0.01mm级的重复定位精度和高速运动性能。

       它的工作范围呈圆柱形，特别适合平面内的高精度操作，广泛应用于电子制造的元器件插装、汽车零部件装配、医疗器械生产及食品包装等场景，与六轴机器人的复杂三维操作、直角坐标机器人的简单直线运动相比，SCARA机器人以在水平高精度任务中的独特优势成为自动化生产线的关键设备。

拉格朗日法

       拉格朗日法在建模中是一种通过构造拉格朗日函数简化复杂系统描述的核心方法，在力学建模中，以动能与势能之差为基础，结合广义坐标和拉格朗日方程推导出运动方程，无需直接处理约束力，高效适配多约束、多自由度系统（如机器人）；在优化建模中，通过引入拉格朗日乘数将目标函数与约束条件融合为统一函数，将带约束极值问题转化为无约束问题求解，广泛应用于工程设计、资源分配等场景，其核心价值在于化繁为简，为系统分析、数值求解和控制设计提供简洁且普适的数学基础。

拉格朗日法的一般步骤：

（1）选定机器人的广义坐标q。虽然广义坐标的选定并不唯一，但是一般地，优先选择D-H方法所确定的运动参数；

（2）确定作用在机器人系统上，并且对系统可以做功的非保守力；

（3）计算机器人系统的总动能K、总势能U以及拉格朗日量L=K-U；

（4）计算拉格朗日公式所需的偏导数；

（5）计算机器人系统的广义力F；

（6）代入使用拉格朗日公式求得系统动力学方程。

本文中，我们将采用拉格朗日公式法建立SCARA机器人的动力学模型。

图1：连杆坐标系布局

图2：连杆质心及位置向量

根据机器人的D-H连杆参数，选定机器人的广义坐标 ,如图1所示。

确定作用在机器人系统上，并且对系统可以做功的非保守力。假设机器人末端与环境的作用力f为0，那么对于SCARA机器人系统而言，“不做功的非保守力”是各关节电机的驱动力，准确地说，是各关节的输入力矩（力）。它们分别T1,T2,T3,是以及T4。计算机器人系统的总动能K和总势能U，然后计算拉格朗日量L。为了计算机器人各连杆的动能和势能，定义机器人各连杆的质心分别为C1、C2、C3和C4，各连杆质心位置矢量分别为pc1、pc2、pc3和pc4，如图2所示。设各连杆的质量分别为m1、m2、m3、m4，连杆1关于其关节轴的惯性矩为I1，连杆i关于其质心坐标系Z轴的惯量矩为Izz。

SCARA机器人各连杆的质心位置向量分别是：

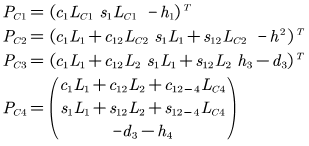
首先计算机器人各连杆的动能：

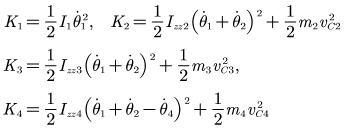
机器人的总动能为K=K1+K2+K3+K4

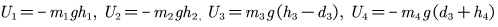
机器人的总势能为U=U1+U2+U3+U4

完成机器人总动能K以及机器人总势能U的计算后，便可以计算拉格朗日量。计算拉格朗日公式所需的偏导数：分别计算拉格朗日L关于各角速度的偏导数，关于时间t的导数，拉格朗日量L关于关节角q的偏导数。

计算机器人系统的广义力F。假设 SCARA机器人各关节发生微小角位移，可以计算在微小位移下机器人所做的虚功：

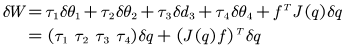
广义力的计算方法为求虚功关于微小角位移的偏导数，即：

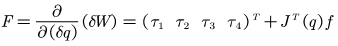
如前文所述，假设机器人末端与环境的作用力f为0，则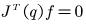，所以SCARA机器人所受到的广义力为：

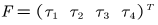
将计算结果所得到的各偏导数结果以及广义力分别代入使用拉格朗日公式：

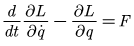
即可求得系统动力学方程。

一般地，机械臂动力学方程的一般形式为：

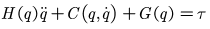
为惯性矩阵，它是一个角对称矩阵，各非零元素的取值大小取决于机器人各关节角的大小。表征机器人所受到的惯性力的大小。

为离心力和科氏力矩阵，表征 SCARA机器人所受到的离心力和科氏力的大小。离心力和科氏力矩阵各非零元素的取值大小取决于机器人各关节角的大小以及各关节角速度的大小。

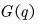为重力矩阵，表征 SCARA机器人所受到的重力的大小。重力矩阵各非零元素的取值大小取决于机器人各关节角的大小。

为关节力矩（力）输入矩阵，表征各轴电机通过传动装置对机器人各关节轴的输入力矩。  

将拉格朗日动力学方程整理成机械臂动力学方程的一般形式，即可获得 SCARA机器人具体的动力学方程：

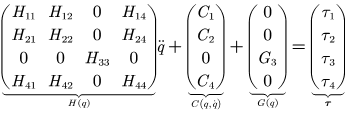
经过上述的推导和分析，我们可以建立起SCARA机器人的动力学方程。

       SCARA 机器人建模既精准捕捉了平面多关节运动的物理特性与动力学规律，同时也为机器人轨迹规划、运动控制及精度优化提供了核心数学框架。以此为依托不断细化模型参数、提升算法适配性，可推动 SCARA 机器人技术向更高速度、更高精度演进，助力其在电子制造、精密装配等更多高精度作业领域释放效能。