深谷技术 | 双摆自起摆稳摆控制策略详解

       针对一阶并联旋转双倒立摆系统，其起摆策略主要分为两种：并行起摆和串行起摆。这两种方法均基于能量控制原理设计，但其实现方式有所不同。串行起摆通过依次减少两个摆杆的能量至零来实现，即先使一个摆杆达到垂直向上的稳定状态（此时假设其能量为零），随后再处理另一个摆杆；而并行起摆则是尝试同步调整两个摆杆的能量，力求同时将两者置于稳定的垂直位置。具体而言，并行起摆试图在同一过程中同时降低长摆杆和短摆杆的能量直至归零；相比之下，串行起摆则分步进行，首先专注于单个摆杆的能量控制，之后再转向下一个。

       如图1.1所示，并行起摆过程示意了同时对两个摆杆进行能量控制的方法；而图1.2则展示了串行起摆的流程，强调了逐步、有序的能量管理。

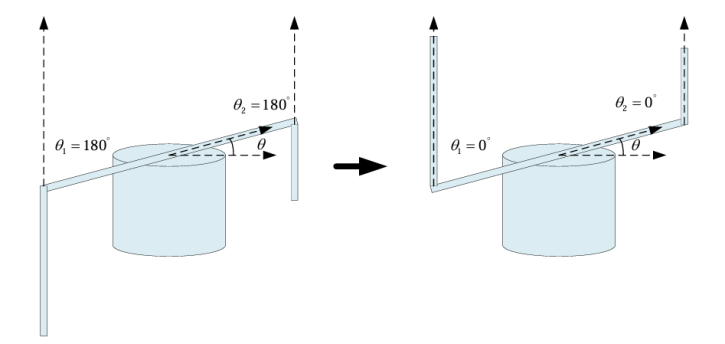
图1.1 并行起摆示意图

图1.2 串行起摆示意

       对于并行起摆控制，理论上存在的误差主要源于长摆杆和短摆杆所遵循的动力学模型的简化。具体而言，并行起摆控制策略在建模过程中通常忽略了高阶项（如二次项）以及系统内的摩擦力，这些简化虽然可以简化控制算法的设计，但也引入了不可避免的控制误差。特别是在本系统中，由于惯性相对较小，旋转臂需要提供较大的角加速度和角速度以实现起摆，这使得系统对任何误差或外界扰动都极为敏感，进一步降低了并行起摆的成功率。

       此外，在惯性较小的情况下，并行起摆要求两个摆杆同步达到稳定状态，这对控制系统提出了极高的精度要求。即使是微小的初始条件差异或者动力学参数估计误差，也可能导致两摆杆之间的相位差增大，最终使并行起摆难以实现。因此，在这种情况下，采用串行起摆策略显得尤为合理。

串行起摆

串行起摆的控制

       过程分为多个有序步骤，通过精确调控旋转臂的角加速度或转矩来间接实现对长摆杆和短摆杆的分阶段控制。这种策略的设计灵感来源于能量法，即分别考虑两个摆杆的能量控制，通过串行处理简化了能量管理的复杂性，并提高了控制精度。串行起摆的控制流程主要包括以下三个关键部分：

长摆杆起摆控制

       首先，控制系统驱动电机调整旋转臂的运动，使长摆杆逐步摆动至垂直向上的位置。在此过程中，重点是通过控制输入（如角加速度或转矩）逐渐减少长摆杆的能量，直至其达到预期的零点状态，即角度偏差为零且稳定不动的位置。此阶段的目标是确保长摆杆能够以最小的能量消耗顺利到达并保持在垂直向上。

长摆杆稳态控制

       当长摆杆接近垂直位置时，整个系统可以被近似视为一个线性的旋转倒立单摆模型。此时，采用线性二次型调节器（LQR）进行优化设计，以实现长摆杆的稳态控制。LQR方法通过对系统动态特性建模，结合性能指标矩阵Q和R的选择，计算出最优的状态反馈增益矩阵K，从而有效抑制任何可能导致长摆杆偏离垂直位置的扰动。这一步骤确保了长摆杆在后续操作中的稳定性，为下一步提供了坚实的基础。

短摆杆起摆及协调控制

       类比于长摆杆的起摆过程，接下来根据能量法启动短摆杆的起摆。值得注意的是，在保证长摆杆已经处于稳态的前提下，期望的系统输入（旋转臂的角加速度或转矩）应当等于短摆杆起摆所需的控制输入与维持长摆杆稳态所需的控制输入之和。由于短摆杆质量较小，其起摆所需的额外输入在整个系统输入中占比相对较低，因此可以在不显著影响整体稳定性的前提下完成短摆杆的起摆。此外，这种方法有助于协调两摆杆之间的相互作用，确保两者都能达到理想的垂直状态，同时最大限度地减少了因相互干扰而可能产生的误差。

       这种串行起摆控制方法可在两个摆杆的能量控制方面做到更加准确，确保倒立摆系统从起摆过程切换到双摆杆稳摆过程时，长摆杆和短摆杆的角度和角速度更小，系统所需要的控制输入变化量会更小，更容易实现在起摆-稳摆之间的成功切换。综上，串行起摆控制方法可优化能量控制的精准性，有效地减小两个摆杆之间的耦合作用，提高一阶并联旋转倒立摆系统中两个摆杆起摆和稳摆成功的可能性。控制器设计

长摆起摆控制

       倒立摆的摆杆起摆本质上是对于倒立摆摆杆能量的控制，使得摆杆的能量逐渐趋近于稳定在垂直向上状态时的能量。

这里假设长摆杆的能量由势能与转动动能之和，即

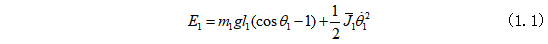
       可以发现倒立摆的摆杆在垂直向上稳定状态时的能量为零。在不考虑倒立摆系统的摩擦影响的情况下，对摆杆的能量对时间求导，可得(忽略摩擦)

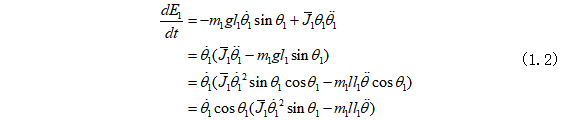
      其中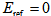。因为李亚普诺夫函数V大于等于零，如果该李亚普诺夫函数导数小于等于零状态的话，那么倒立摆摆杆的能量将会收敛到零，即摆杆会到达角度为零且角速度为零的平衡状态。

对李亚普诺夫函数求导，可以得到其导数为式(1.4)，为了保证实现起摆控制，那么就可以假设系统输入为式(1.5)。

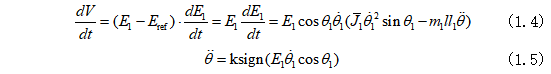
       在上述的条件下，李雅普诺夫函数的导数小于等于零

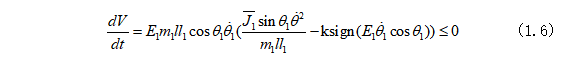
       其中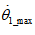为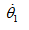绝对值的最大值，同样假设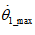满足如下条件

       由上述推导可以得出，倒立摆的旋转臂加速度为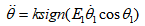时，可以实现旋转倒立摆系统中单个摆杆的起摆控制。

长摆稳摆控制

       在一阶并联旋转倒立摆系统中的长摆杆完成起摆控制之后，倒立摆系统的长摆杆能量最终接近于零，也就是接近于垂直向上的状态，此时系统可近似看为线性系统，控制器可以切换到常见的线性系统控制方法，以实现长摆杆的稳摆控制；其中，线性二次型最优调节器 (LQR) 是常用的线性系统控制方法，它具有设计简单，控制效果良好的特点。这里选择使用LQR设计PRIDP系统长摆杆的稳摆控制器，实现长摆杆的稳摆控制，保证后续时刻长摆杆的摆角都稳定在接近于零的状态。由于这里的倒立摆系统的被控变量(系统控制输入)是旋转臂的角加速度，所以LQR控制器的设计可忽略短摆杆的存在(即不考虑两摆杆之间的耦合作用)，因为理论上来说，在以旋转臂的角加速度为控制输入的情况下，短摆的状态不会对系统的输入造成影响，也就不会对另一侧的长摆杆的稳摆控制造成影响。在实际系统控制中，系统的控制不是那么理想，但是由于短摆自身质量、转动惯量等属性较小，对系统长摆杆的稳摆控制影响也较小，因此在实现长摆稳摆控制时可忽略短摆的影响，将一阶并联旋转倒立摆系统视为旋转倒立单摆来看即可。在以旋转臂的角加速度为控制输入的情况下，长摆杆的稳摆控制可线性化为如下的状态控制方程的形式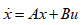，其中

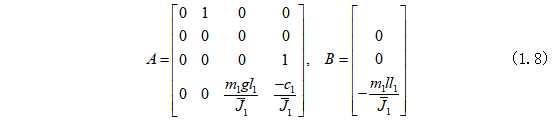
      为了实现长摆杆从起摆到稳摆的顺利切换，需要设计适当的Q矩阵和R矩阵。可以实现对倒立摆系统的有效控制，使得长摆杆在满足切换条件的情况下实现从起摆过程到稳摆过程的平稳过渡。

短摆起摆控制

       串行起摆的最后一步是实现短摆杆的起摆，让短摆杆的角度接近零；我们之所以让短摆后起摆，是因为长摆惯性较大，长摆稳摆之后更不容易失去平衡。此过程中比较困难的是要通过控制旋转臂的角加速度实现在长摆杆稳定的情况下保证短摆杆能量逐渐递减(摆角趋于零)，从而使得短摆杆逐渐到达可以进行双摆杆的稳摆控制状态。长摆杆稳摆使用的是LQR，短摆杆起摆是基于能量法。可以根据倒立摆系统的状态求出长摆杆稳摆所需要的系统控制输入a1和短摆杆起摆所需的系统控制输入a2。这里采用的方法是将长摆杆LQR稳摆控制的角加速度a1和短摆起摆所需的角加速度a2进行叠加，并通过让电机按照叠加得到的角加速度a运行来实现长摆杆稳摆+短摆杆起摆的控制状态。假设短摆杆的能量E2也同样由重力势能和转动动能组成，则假设E2可以表示为式(1.9)，同样假设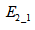如式(1.10)：

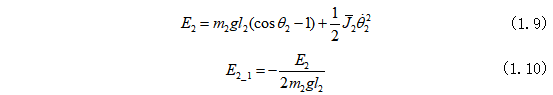
在这一过程中，短摆杆起摆的系统输入a1可视为长摆杆稳摆过程中的扰动，所以关键是确保长摆杆的稳摆算法具有较好的鲁棒性，即使在引入短摆起摆这个外部扰动a2的情况下，仍能有效实现长摆杆的稳摆控制。同时，为了保证双摆稳摆控制器在切换时短摆杆的角度和角速度不会过大，这里将一阶并联旋转倒立摆系统的短摆杆的起摆需要的旋转臂角加速度与其能量之间进行关系关联，需要手动调节参数k1和k2。则短摆杆起摆过程的旋转臂角加速度为

       对于串行起摆而言，理论上存在的误差是在短摆杆的起摆阶段；在此阶段一方面要保证长摆杆稳摆，另一方面又要保证短摆杆的起摆；实际系统的控制输入是将长摆杆稳摆所需的系统控制输入和短摆起摆所需的系统控制输入直接叠加而成，长摆杆稳摆部分可视为输入的主体，短摆起摆部分可视为输入中的扰动，扰动部分负责实现短摆杆起摆。在实际的调试过程中，还需要调整起摆部分的参数，以保证既不影响长摆杆稳摆又能保证短摆杆起摆。因此当一阶并联旋转双倒立摆的短摆杆长度比较小时，串行起摆误差会比较小，容易实现串行起摆控制。